Relationships Between Equations of Power
- Samuel Yong
- Mar 29, 2020
- 3 min read
Updated: Apr 11, 2020
There are quite a few equations one could possibly use to calculate Power. These are set out below:
List of Equations for Calculating Power
(a) Power = Energy / Time
(b) Power = Force x Velocity
(c) Power = Voltage x Current
(d) Power = Current^2 x Resistance
(e) Power = Voltage^2 / Resistance
It is uncommon for a single physical quantity to have these many equations, and a considerable effort would be required to memorize all of them. However, one need not memorize all of them. Rather, you can simply memorize a few and derive the rest. Here is how:
Step 1: Begin with the following equations:
Power = Energy / Time - - - (1)
Voltage = Current x Resistance - - - (2)
Step 2: Manipulate equation (1), replacing Energy with Work Done:
From equation (1),
Power = Energy / Time
Power = Work Done / Time
Power = (Force x Displacement) / Time
Power = Force x (Displacement / Time)
Power = Force x Velocity - - - (3)
We have obtained equation (3) from equation (1) by replacing Energy with Work Done. However, you may be wondering whether it is appropriate to conflate the two. To address this concern, the definitions of those two physical quantities are set out below:
Energy is the ability to do work.
Work done is the energy converted from one form to another when a force causes an object to be displaced.
As such, Work Done is a subset of Energy, so it is not wrong to replace Energy with Work Done as shown above.
Also, Velocity is the rate of change of Displacement (often with respect to Time). Hence Displacement / Time can be replaced with Velocity.
Step 3: Manipulate equation (1) by inserting Charge without changing the values of any algebraic expressions:
From equation (1),
Power = Energy / Time
Power = Work Done / Time
Power = (Work Done / 1) x (1 / Time)
Power = (Work Done / Charge) x (Charge / Time)
Power = Voltage x Current - - - (4)
As such, we can obtain equation (4) from equation (1) by first replacing energy with work done before introducing charge. The key doing it right is to insert charge without changing the resulting value of the algebraic expressions on either side of the equation.
Charge was inserted above by dividing Work Done by Charge, and multiplying (1 / Time) by Charge. As dividing by Charge and multiplying by Charge are opposite functions of one another, they cancel each other out. Hence inserting both functions at the same time does not change the value of any algebraic expression.
Next, Work Done/Charge was replaced by Voltage, while Charge/Time was replaced by Current. The definitions of Voltage and Current are set out below:
Voltage is the work done to move a unit charge from one point to another in a circuit.
Current is the rate of flow of electric charge.
As such, Voltage = Work Done / Charge, and Current = Charge / Time.
Step 4: Substitute equation (2) into equation (4)
Voltage = Current x Resistance - - - (2)
Power = Voltage x Current - - - (4)
After substituting equation (2) into equation (4),
Power = Current x Resistance x Current
Power = Current x Current x Resistance
Power = Current^2 x Resistance - - - (5)
Step 5: Manipulate equation (2) to obtain a new equation, substitute that new equation into equation (4)
From equation (2),
Voltage = Current x Resistance
Voltage / Resistance = (Current x Resistance) / Resistance
Voltage / Resistance = Current
Current = Voltage / Resistance - - - (6)
Power = Voltage x Current - - - (4)
After substituting equation (6) into equation (4),
Power = Voltage x (Voltage / Resistance)
Power = Voltage^2 / Resistance - - - (7)
As such, instead of memorizing all five equations of power, you can just memorize equations (1) and (2) and derive the rest! A map of the workings of simultaneous equations above is set out below:
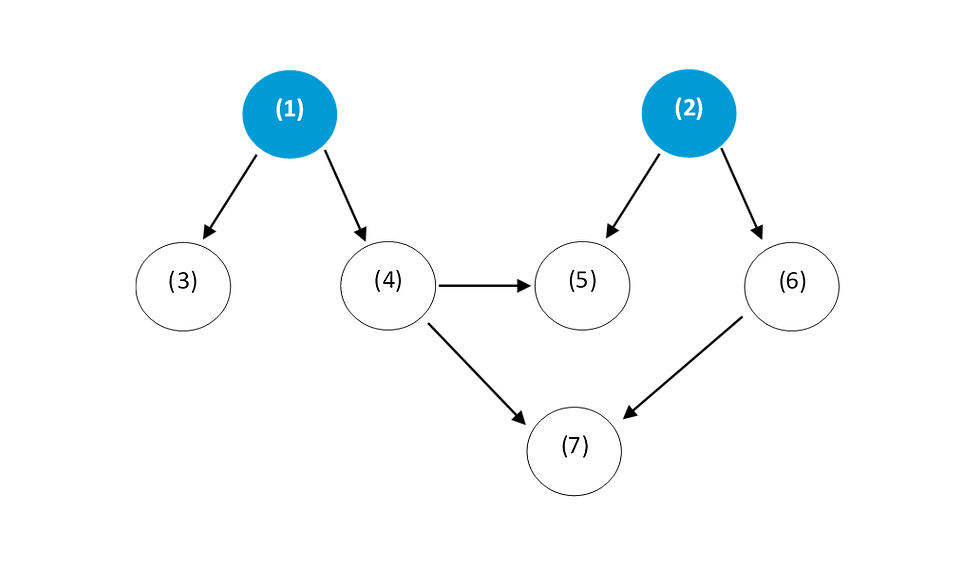

Comentarios